Pre-service teachers using an app to generalize figural patterns through figural reasoning

Jørgen Sjaastad; Carl Andreas Lorange

doi:10.31129/LUMAT.14.1.2856

Authors

Jørgen Sjaastad NLA University College, Norway https://orcid.org/0000-0003-1543-8518
Carl Andreas Lorange NLA University College, Norway https://orcid.org/0000-0003-0856-4129

DOI:

https://doi.org/10.31129/LUMAT.14.1.2856

Keywords:

algebraic thinking, dynamic learning environment, figure patterns, generalizations

Abstract

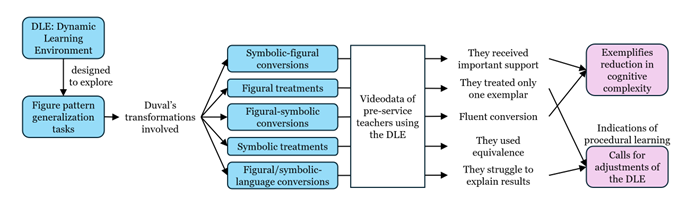
To investigate a dynamic learning environment’s (DLE) facilitation of students’ figural generalization of figural patterns, this study scrutinizes 12 pre-service teachers’ efforts to generalize figural patterns using a DLE that offers dynamically adapting shapes. The shapes support identification of figural patterns’ figural commonalities. In video recorded task-based interviews, the pre-service teachers worked in pairs to solve figural pattern tasks using the DLE. Duval’s (2006) theory of semiotic representations is utilized to identify characteristics of the pre-service teachers’ conversions and treatments. Results show that they adopted an experimental approach and utilized the DLE to create multiple valid symbolic generalizations, and they used symbolic treatments to support some solutions. However, they would often treat only one exemplar of the figural pattern, weakening the basis for their generalizations, and they struggled to express verbally the figural patterns’ generalized structure. These results raise concerns about the algebraic thinking involved in their solution processes. Implications of this study include the identification of crucial factors of DLEs designed to support students’ exploration of figural patterns.

References

Becker, J. R., & Rivera, F. (2005). Generalization strategies of beginning high school algebra students. In H. L. Chick & J. L. Vincent (Eds.), Proceedings of the 29th conference of the International Group for the Psychology of Mathematics Education (pp. 121–128). PME.

Bills, L., & Rowland, T. (1999). Examples, generalisation and proof. Research in Mathematics Education, 1(1), 103–116. https://doi.org/10.1080/14794809909461549 DOI: https://doi.org/10.1080/14794809909461549

Bråting, K., & Kilhamn, C. (2021). Exploring the intersection of algebraic and computational thinking. Mathematical Thinking and Learning, 23(2), 170–185. https://doi.org/10.1080/10986065.2020.1779012 DOI: https://doi.org/10.1080/10986065.2020.1779012

Duval, R. (1998). Geometry from a cognitive point of view. In C. Mammana & V. Villani (Eds.), Perspectives on the teaching of geometry for the 21st century (Vol. 21, pp. 37–52). Kluwer.

Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103–131. https://doi.org/10.1007/s10649-006-0400-z DOI: https://doi.org/10.1007/s10649-006-0400-z

Dyrvold, A., & Bergvall, I. (2023). Static, dynamic and interactive elements in digital teaching materials in mathematics: How do they foster interaction, exploration and persistence? LUMAT Special Issue, 11(3), 103–131. https://doi.org/https://doi.org/10.31129/LUMAT.11.3.1941 DOI: https://doi.org/10.31129/LUMAT.11.3.1941

Dörfler, W. (1991). Forms and means of generalization in mathematics. In A. Bishop, S. Mellin-Olsen, & J. v. Dormolen (Eds.), Mathematical knowledge: Its growth through teaching (pp. 61–85). Springer. DOI: https://doi.org/10.1007/978-94-017-2195-0_4

El Mouhayar, R. (2018). Trends of progression of student level of reasoning and generalization in numerical and figural reasoning approaches in pattern generalization. Educational Studies in Mathematics, 99(1), 89–107. https://doi.org/https://doi.org/10.1007/s10649-018-9821-8 DOI: https://doi.org/10.1007/s10649-018-9821-8

El Mouhayar, R., & Jurdak, M. (2015). Variation in strategy use across grade level by pattern generalization types. International Journal of Mathematical Education in Science and Technology, 46(4), 553–569. https://doi.org/https://doi.org/10.1080/0020739X.2014.985272 DOI: https://doi.org/10.1080/0020739X.2014.985272

El Mouhayar, R., & Jurdak, M. (2016). Variation of student numerical and figural reasoning approaches by pattern generalization type, strategy use and grade level. International Journal of Mathematical Education in Science and Technology, 47(2), 197–215. https://doi.org/10.1080/0020739X.2015.1068391 DOI: https://doi.org/10.1080/0020739X.2015.1068391

Ellis, A. B., & Özgür, Z. (2024). Trends, insights, and developments in research on the teaching and learning of algebra. ZDM Mathematics Education, 56(2), 199–210. https://doi.org/https://doi.org/10.1007/s11858-023-01545-9 DOI: https://doi.org/10.1007/s11858-023-01545-9

Healy, L., & Hoyles, C. (1999). Visual and symbolic reasoning in mathematics: Making connections with computers? Mathematical Thinking and Learning, 1(1), 59–84. https://doi.org/https://doi.org/10.1207/s15327833mtl0101_3 DOI: https://doi.org/10.1207/s15327833mtl0101_3

Hewitt, D. (1998). Approaching arithmetic algebraically. Mathematics Teaching, 163, 19–29.

Hewitt, D. (2019, Feb). “Never carry out any arithmetic”: the importance of structure in developing algebraic thinking. Presentation at CERME 11 - Eleventh Congress of the European Society for Research in Mathematics Education. ERME.

Jackson, J. L., & Stenger, C. L. (2024). Methods of explicitly teaching generalization in the mathematics classroom and indicators of success: A systematic review. International Journal of Education in Mathematics, Science and Technology, 12(4), 1109–1126. https://doi.org/https://doi.org/10.46328/ijemst.4171 DOI: https://doi.org/10.46328/ijemst.4171

Küchemann, D. (2010). Using patterns generically to see structure. Pedagogies: an international journal, 5(3), 233–250. https://doi.org/10.1080/1554480X.2010.486147 DOI: https://doi.org/10.1080/1554480X.2010.486147

Lannin, J. K. (2005). Generalization and justification: The challenge of introducing algebraic reasoning through patterning activities. Mathematical Thinking and Learning, 7(3), 231–258. https://doi.org/10.1207/s15327833mtl0703_3 DOI: https://doi.org/10.1207/s15327833mtl0703_3

Leung, A., Baccaglini-Frank, A., & Mariotti, M. A. (2013). Discernment of invariants in dynamic geometry environments. Educational Studies in Mathematics, 84, 439–460. https://doi.org/https://link.springer.com/article/10.1007/s10649-013-9492-4 DOI: https://doi.org/10.1007/s10649-013-9492-4

Mason, J. (1996). Expressing generality and roots of algebra. In N. Bernarz, C. Kieran, & L. Lee (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 65–86). Springer. https://doi.org/https://doi.org/10.1007/978-94-009-1732-3_5 DOI: https://doi.org/10.1007/978-94-009-1732-3_5

Montenegro, P., Costa, C., & Lopes, B. (2018). Transformations in the visual representation of a figural pattern. Mathematical Thinking and Learning, 20(2), 91–107. https://doi.org/https://doi.org/10.1080/10986065.2018.1441599 DOI: https://doi.org/10.1080/10986065.2018.1441599

Montenegro, P., Costa, C., & Lopes, J. B. (2019). Improving visual representations' impact in mathematics teaching with multimodal narratives. In J. Lopes, M. C. Viegas, & J. A. Pinto (Eds.), Multimodal Narratives in Research and Teaching Practices (pp. 211–230). IGI Global. https://doi.org/10.4018/978-1-5225-8570-1 DOI: https://doi.org/10.4018/978-1-5225-8570-1.ch010

Pearce, D., Mavrikis, M., Geraniou, E., & Gutiérrez, S. (2008). Issues in the design of an environment to support the learning of mathematical generalisation. In P. Dillenbourg & M. Specht (Eds.), European conference on technology enhanced learning (pp. 326–337). Springer. https://doi.org/10.1007/978-3-540-87605-2_37 DOI: https://doi.org/10.1007/978-3-540-87605-2_37

Radford, L. (2008). Iconicity and contraction: A semiotic investigation of forms of algebraic generalizations of patterns in different contexts. ZDM Mathematics Education, 40(1), 83–96. https://doi.org/10.1007/s11858-007-0061-0 DOI: https://doi.org/10.1007/s11858-007-0061-0

Radford, L. (2010). Layers of generality and types of generalization in pattern activities. PNA. Revista de Investigación en Didáctica de la Matemática, 4(2), 37–62. https://doi.org/https://doi.org/10.30827/pna.v4i2.6169 DOI: https://doi.org/10.30827/pna.v4i2.6169

Radford, L., & Peirce, C. S. (2006). Algebraic thinking and the generalization of patterns: A semiotic perspective. In S. Alatorre, J. L. Cortina, M. Sáiz, & A. Méndez (Eds.), Proceedings of the 28th conference of the international group for the psychology of mathematics education, North American chapter (Vol. 1, pp. 2–21). PME-NA.

Rivera, F., & Becker, J. R. (2007). Abduction–induction (generalization) processes of elementary majors on figural patterns in algebra. The Journal of Mathematical Behavior, 26(2), 140–155. https://doi.org/https://doi.org/10.1016/j.jmathb.2007.05.001 DOI: https://doi.org/10.1016/j.jmathb.2007.05.001

Rivera, F., & Becker, J. R. (2008). Middle school children’s cognitive perceptions of constructive and deconstructive generalizations involving linear figural patterns. ZDM Mathematics Education, 40, 65–82. https://doi.org/10.1007/s11858-007-0062-z DOI: https://doi.org/10.1007/s11858-007-0062-z

Ruthven, K. (2018). Instructional activity and student interaction with digital resources. In L. Fan, L. Trouche, C. Qi, S. Rezat, & J. Visnovska (Eds.), Research on mathematics textbooks and teachers’ resources: advances and issues (pp. 261–275). Springer. https://doi.org/https://doi.org/10.1007/978-3-319-73253-4_12 DOI: https://doi.org/10.1007/978-3-319-73253-4_12

Yao, X. (2022). Representation transformations in transition from empirical to structural generalization. The Journal of Mathematical Behavior, 66, 100964. https://doi.org/https://doi.org/10.1016/j.jmathb.2022.100964 DOI: https://doi.org/10.1016/j.jmathb.2022.100964

Yao, X., & Elia, J. (2021). Connections between empirical and structural reasoning in technology-aided generalization activities. International Electronic Journal of Mathematics Education, 16(2). https://doi.org/https://doi.org/10.29333/iejme/9770 DOI: https://doi.org/10.29333/iejme/9770

Yeo, S., & Webel, C. (2024). Elementary students’ fraction reasoning: a measurement approach to fractions in a dynamic environment. Mathematical Thinking and Learning, 26(1), 20–46. https://doi.org/https://doi.org/10.1080/10986065.2022.2025639 DOI: https://doi.org/10.1080/10986065.2022.2025639