Beyond the dichotomy: Deeds and explorations as a mutually enhancing dyad in undergraduate mathematics education

Ninni Marie Hogstad; Olov Viirman

doi:10.31129/LUMAT.13.1.2957

Authors

Ninni Marie Hogstad University of Agder, Norway https://orcid.org/0000-0001-6552-0822
Olov Viirman Uppsala Universitet, Sweden https://orcid.org/0000-0002-4909-1914

DOI:

https://doi.org/10.31129/LUMAT.13.1.2957

Keywords:

commognitive framework, explorative routines, deed-oriented routines, animation tool

Abstract

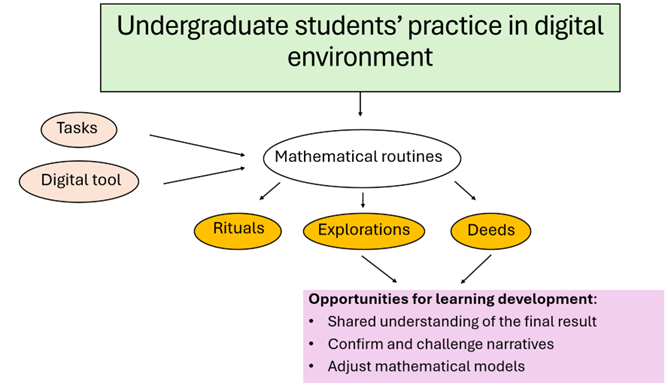
Students’ development of routines is essential to learning, particularly in STEM studies where there is a goal of preparing students for directly applying mathematics for practical ends. We hypothesize that this impacts on how they engage with routines. We report from an empirical study which explores different types of routines that undergraduate students engage in when using an animation tool to model motion in a real-world context. Drawing on commognitive theory, we conducted a fine-grained qualitative analysis of the discursive activity of one group of three engineering students. Rather than aiming for a broad generalization, the study uses this dataset to examine the mechanisms through which students shift between deed-oriented and explorative routines. The analysis shows that these routines do not function as separate forms of engagement, rather they developed as a mutually reinforcing dyad – a dyadic relationship. We argue that recognizing this relationship provides a refined lens for understanding how environments may support possibilities not only for practical learning, but also for discursive learning.

References

Baccaglini-Frank, A. (2021). To tell a story, you need a protagonist: how dynamic interactive mediators can fulfill this role and foster explorative participation to mathematical discourse. Educational Studies in Mathematics, 106(2), 291–312. https://doi.org/10.1007/s10649-020-10009-w DOI: https://doi.org/10.1007/s10649-020-10009-w

Biza, I. (2021). The discursive footprint of learning across mathematical domains: The case of the tangent line. The Journal of Mathematical Behavior, 62(1), 100870. https://doi.org/10.1016/j.jmathb.2021.100870 DOI: https://doi.org/10.1016/j.jmathb.2021.100870

Cooper, J., & Lavie, I. (2021). Bridging incommensurable discourses – A commognitive look at instructional design in the zone of proximal development. The Journal of Mathematical Behavior, 61(1), 100822. https://doi.org/10.1016/j.jmathb.2020.100822 DOI: https://doi.org/10.1016/j.jmathb.2020.100822

Gainsburg, J. (2006). The Mathematical Modeling of Structural Engineers. Mathematical Thinking and Learning, 8(1), 3–36. https://doi.org/10.1207/s15327833mtl0801_2 DOI: https://doi.org/10.1207/s15327833mtl0801_2

Geiger, V. (2017). Designing for Mathematical Applications and Modelling Tasks in Technology Rich Environments. In A. Leung & A. Baccaglini-Frank (Eds.), Digital Technologies in Designing Mathematics Education Tasks: Potential and Pitfalls (pp. 285–301). Springer International Publishing. https://doi.org/10.1007/978-3-319-43423-0_14 DOI: https://doi.org/10.1007/978-3-319-43423-0_14

González-Martín, A. S. (2021). VB-VA= ʃf(x)dx. The Use of Integrals in Engineering Programmes: a Praxeological Analysis of Textbooks and Teaching Practices in Strength of Materials and Electricity and Magnetism Courses. International Journal of Research in Undergraduate Mathematics Education, 7(2), 211–234. https://doi.org/10.1007/s40753-021-00135-y DOI: https://doi.org/10.1007/s40753-021-00135-y

González-Martín, A. S., Barquero, B., & Gueudet, G. (2022). Mathematics in the Training of Engineers: Contributions of the Anthropological Theory of the Didactic. In R. Biehler, M. Liebendörfer, G. Gueudet, C. Rasmussen, & C. Winsløw (Eds.), Practice-Oriented Research in Tertiary Mathematics Education (pp. 559–579). Springer International Publishing. https://doi.org/10.1007/978-3-031-14175-1_27 DOI: https://doi.org/10.1007/978-3-031-14175-1_27

Heyd-Metzuyanim, E., Smith, M., Bill, V., & Resnick, L. B. (2018). From ritual to explorative participation in discourse-rich instructional practices: a case study of teacher learning through professional development. Educational Studies in Mathematics. https://doi.org/10.1007/s10649-018-9849-9 DOI: https://doi.org/10.1007/s10649-018-9849-9

Hiebert, J., & Lefevre, P. (1986). Conceptual and procedural knowledge in mathematics: An introductory analysis. In J. Hiebert (Ed.), Conceptual and Procedural Knowledge: The Case of Mathematic (pp. 1–27). Erlbaum, Hillsdale, NJ.

Kontorovich, I. (2021). Pre-university students square-root from squared things: A commognitive account of apparent conflicts within learners' mathematical discourses. The Journal of Mathematical Behavior, 64(4), 100910. https://doi.org/10.1016/j.jmathb.2021.100910 DOI: https://doi.org/10.1016/j.jmathb.2021.100910

Lavie, I., & Sfard, A. (2019). How Children Individualize Numerical Routines: Elements of a Discursive Theory in Making. Journal of the Learning Sciences, 28(4-5), 419–461. https://doi.org/10.1080/10508406.2019.1646650 DOI: https://doi.org/10.1080/10508406.2019.1646650

Lavie, I., Steiner, A., & Sfard, A. (2019). Routines we live by: From ritual to exploration. Educational Studies in Mathematics, 101(2), 153–176. https://doi.org/10.1007/s10649-018-9817-4 DOI: https://doi.org/10.1007/s10649-018-9817-4

Loch, B., & Lamborn, J. (2016). How to make mathematics relevant to first-year engineering students: perceptions of students on student-produced resources. International Journal of Mathematical Education in Science and Technology, 47(1), 29–44. https://doi.org/10.1080/0020739X.2015.1044043 DOI: https://doi.org/10.1080/0020739X.2015.1044043

Maass, K., Geiger, V., Ariza, M. R., & Goos, M. (2019). The Role of Mathematics in interdisciplinary STEM education. ZDM, 51(6), 869–884. https://doi.org/10.1007/s11858-019-01100-5 DOI: https://doi.org/10.1007/s11858-019-01100-5

Nachlieli, T., & Tabach, M. (2012). Growing mathematical objects in the classroom – The case of function. International Journal of Educational Research, 51–52(1), 10–27. https://doi.org/10.1016/j.ijer.2011.12.007 DOI: https://doi.org/10.1016/j.ijer.2011.12.007

Nachlieli, T., & Tabach, M. (2019). Ritual-enabling opportunities-to-learn in mathematics classrooms. Educational Studies in Mathematics, 101(2), 253–271. https://doi.org/10.1007/s10649-018-9848-x DOI: https://doi.org/10.1007/s10649-018-9848-x

Nunes, T., & Bryant, P. (1996). Children doing mathematics. Blackwell Publishers.

Oliver, R. (2000). When teaching meets learning: Design principles and strategies for Web-based learning environments that support knowledge construction. In R. Sims, M. O’Reilly, & S. Sawkins (Eds.), Learning to choose. Choosing to learn. Proceedings of the Australian Society for Computers in Learning in Tertiary Education 2000 conference (pp. 17–28).

Schmidt, K., & Winsløw, C. (2021). Authentic Engineering Problems in Service Mathematics Assignments: Principles, Processes and Products from Twenty Years of Task Design. International Journal of Research in Undergraduate Mathematics Education, 7(2), 261–283. https://doi.org/10.1007/s40753-021-00133-0 DOI: https://doi.org/10.1007/s40753-021-00133-0

Sfard, A. (2005). What changes when learning goes to school: The communicational version, the case of mathematics. European Journal of School Psychology, 3(1), 301–326.

Sfard, A. (2008). Thinking as communicating. Cambridge University Press. DOI: https://doi.org/10.1017/CBO9780511499944

Sfard, A., & Lavie, I. (2005). Why Cannot Children See as the Same What Grown-Ups Cannot See as Different?— Early Numerical Thinking Revisited. Cognition and Instruction, 23(2), 237–309. https://doi.org/10.1207/s1532690xci2302_3 DOI: https://doi.org/10.1207/s1532690xci2302_3

Stillman, G., Brown, J., & Czocher, J. (2020). Yes, mathematicians do X so students should do X, but it’s not the X you think! ZDM, 52(6), 1211–1222. https://doi.org/10.1007/s11858-020-01183-5 DOI: https://doi.org/10.1007/s11858-020-01183-5

Sullivan, P. (2011). Teaching mathematics: Using research-informed strategies. Camberwell: ACER.

Tabach, M., & Nachlieli, T. (2015). Classroom engagement towards using definitions for developing mathematical objects: the case of function. Educational Studies in Mathematics, 90(2), 163–187. http://dx.doi.org/10.1007/s10649-015-9624-0 DOI: https://doi.org/10.1007/s10649-015-9624-0

Viirman, O., & Nardi, E. (2017). From ritual to exploration: The evolution of biology students’ mathematical discourse through mathematical modelling activities. In T. Dooley, & Gueudet, G. (Ed.), Proceedings of the Tenth Congress of the European Society for Research in Mathematics Education (CERME10, February 1-5, 2017, pp. 2274–2281). Dublin, Ireland: DCU Institute of Education and ERME. https://hal.archives-ouvertes.fr/hal-01941308

Viirman, O., & Nardi, E. (2018). Ritualised and exploratory graphing routines in mathematical modelling: The Digoxin task. In E. Bergqvist, Österholm, M., Granberg, C., & Sumpter, L. (Ed.), Proceedings of the 42nd Conference of the International Group for the Psychology of Mathematics Education (Vol. 4, pp. 363–370). Umeå, Sweden: PME.

Viirman, O., & Nardi, E. (2019). Negotiating different disciplinary discourses: biology students’ ritualized and exploratory participation in mathematical modeling activities. Educational Studies in Mathematics, 101(2), 233–252. https://doi.org/10.1007/s10649-018-9861-0 DOI: https://doi.org/10.1007/s10649-018-9861-0

Viirman, O., & Nardi, E. (2021). Running to keep up with the lecturer or gradual de-ritualization? Biology students’ engagement with construction and data interpretation graphing routines in mathematical modelling tasks. The Journal of Mathematical Behavior, 62(1), 100858. https://doi.org/10.1016/j.jmathb.2021.100858 DOI: https://doi.org/10.1016/j.jmathb.2021.100858

Wood, M. B. (2016). Rituals and right answers: barriers and supports to autonomous activity. Educational Studies in Mathematics, 91(3), 327–348. https://doi.org/10.1007/s10649-015-9653-8 DOI: https://doi.org/10.1007/s10649-015-9653-8