Primary school students’ problem-solving strategies in creating artworks with GeoGebra: Integrating computational thinking skills into mathematics and visual arts lessons

Wahid Yunianto; Daniel Jarvis; Zsolt Lavicza; Zetra Hainul Putra; Shereen El-Bedewy

doi:10.31129/LUMAT.13.2.2547

Authors

Wahid Yunianto Johannes Kepler University Linz, Austria https://orcid.org/0000-0003-1693-6383
Daniel Jarvis Nipissing University, Canada https://orcid.org/0000-0001-9430-3034
Zsolt Lavicza Johannes Kepler University Linz, Austria https://orcid.org/0000-0002-3701-5068
Zetra Hainul Putra University of Riau, Indonesia https://orcid.org/0000-0002-0860-1076
Shereen El-Bedewy Johannes Kepler University Linz, Austria

DOI:

https://doi.org/10.31129/LUMAT.13.2.2547

Keywords:

computational thinking, mathematics, textual programming, GeoGebra, visual arts

Abstract

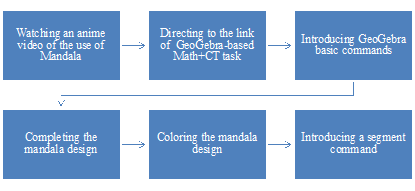
Computational thinking (CT) as a problem-solving skill has been argued to be an essential skill for all learners. Accordingly, there have been efforts to formalize and operationalize CT within school curricula in various countries. In primary schools, students often develop CT through unplugged activities and visual programming activities. However, in this study, we investigated the use of mathematical software with which students typed in commands (codes) to construct artistic artifacts. Educational Design Research (EDR) has guided the development of our task. We attempted to utilize technology to support students’ problem-solving skills and creativity by developing a GeoGebra-based Math+CT task infusing arts. Fifteen Grade 5 primary school students worked on a task to construct a mandala (Hinduism-Buddhism sacred geometrical figures) involving mathematical concepts. Data, in the form of students’ GeoGebra (i.e., “ggb”) files and screen video recordings, were collected and then analyzed using a content analysis method. Findings revealed that our designed task had promoted students’ different problem-solving strategies while working with technology. Additionally, most students did not encounter serious problems in working with GeoGebra commands, and students’ computational thinking skills were supported as a result of engagement with our activities.

References

Alsarayreh, R. S. (2023). The effect of technological skills on developing problem solving skills: The moderating role of academic achievement. International Journal of Instruction, 16(2), 269–388. https://doi.org/10.29333/iji.2023.16221a DOI: https://doi.org/10.29333/iji.2023.16221a

Angeli, E., Cholevas, C., Mavrikos, E., Chatzistamatis, S., & Tsekouras, G. E. (2023). Computational creativity under the framework of recoloring art paintings for color-blindness. 14th International Conference on Information, Intelligence, Systems and Applications, IISA 2023, 1–6. https://doi.org/10.1109/IISA59645.2023.10345967 DOI: https://doi.org/10.1109/IISA59645.2023.10345967

Bakker, A. (2018). Design research in education: A practical guide for early career researchers. In A. Bakker (Ed.), Design research in education: A practical guide for early career researchers (1st ed.). Routledge. https://doi.org/10.4324/9780203701010 DOI: https://doi.org/10.4324/9780203701010

Bocconi, S., Chioccariello, A., Dettori, G., Ferrari, A., & Engelhardt, K. (2016). Developing computational thinking in compulsory education - Implications for policy and practice (P. Kampylis & Y. Punie, Eds.). Publications Office of the European Union. https://doi.org/10.2791/792158

Bocconi, S., Chioccariello, Augusto Kampylis, P., Dagienė, V., Wastiau, P., Engelhardt, K., Earp, J., Horvath, M., Jasutė, E., Malagoli, C., Masiulionytė-Dagienė, V., & Stupurienė, G. (2022). Reviewing computational thinking in compulsory education (A. I. dos Santos, R. Cachia, N. Giannoutsou, & Y. Punie, Eds.). Publications Office of the European Union. https://doi.org/10.2760/126955

Brennan, K., & Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. Proceedings of the 2012 Annual Meeting of the American Educational Research Association, 1–25.

Britannica. (2023). Mandala. In The Editors of Encyclopaedia. Encyclopaedia Britannica. https://www.britannica.com/topic/mandala-diagram

Broley, L., Buteau, C., Modeste, S., Rafalska, M., & Stephens, M. (2024). Computational thinking and mathematics. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education (pp. 323–360). Springer Nature. https://doi.org/10.1007/978-3-031-45667-1_12 DOI: https://doi.org/10.1007/978-3-031-45667-1_12

Chan, S. W., Looi, C. K., Ho, W. K., & Kim, M. S. (2022). Tools and approaches for integrating computational thinking and mathematics: A scoping review of current empirical studies. Journal of Educational Computing Research, 60(8), 2036–2080. https://doi.org/10.1177/07356331221098793 DOI: https://doi.org/10.1177/07356331221098793

Chytas, C., van Borkulo, S. P., Drijvers, P., Barendsen, E., & Tolboom, J. L. J. (2024). Computational thinking in secondary mathematics education with GeoGebra: Insights from an intervention in calculus lessons. Digital Experiences in Mathematics Education, 10, 228–259. https://doi.org/10.1007/s40751-024-00141-0 DOI: https://doi.org/10.1007/s40751-024-00141-0

Dakers, J. R. (2024). What is technology education? LUMAT: International Journal on Math, Science and Technology Education, 11(4), 1–10. https://doi.org/10.31129/LUMAT.11.4.2207 DOI: https://doi.org/10.31129/LUMAT.11.4.2207

Erdem, E., & Kalelioğlu, F. (2024). Comparing traditional and flipped classrooms in teaching block-based programming: Effects on fifth-graders’ self-efficacy towards computational thinking skills, conceptual learning, and their perspectives. Education 3-13, 1–23. https://doi.org/10.1080/03004279.2024.2400933 DOI: https://doi.org/10.1080/03004279.2024.2400933

Fauzan, A. (2002). Traditional mathematics education vs . realistic mathematics education: Hoping for changes. In P. Valero & O. Skovsmose (Eds.), P. Valero &The 3rd International Mathematics Education and Society Conference (pp. 1–4). Danmarks Pædagogiske Universitet.

FISME. (2015, August). IMPOME (International Master Programme on Mathematics Education): master theses of the group 2010-2014. http://www.fisme.science.uu.nl/en/impome/

Grover, S., & Pea, R. (2013). Computational thinking in K-12: a review of the state of the field. Educational Researcher, 42(1), 38–43. https://doi.org/10.3102/0013189X12463051 DOI: https://doi.org/10.3102/0013189X12463051

Hermans, F., & Aivaloglou, E. (2017). A controlled experiment comparing plugged first and unplugged first programming lessons. Proceedings of the 12th Workshop on Primary and Secondary Computing Education, 49–56. https://doi.org/10.1145/3137065.3137072 DOI: https://doi.org/10.1145/3137065.3137072

Hsieh, H. F., & Shannon, S. E. (2005). Three approaches to qualitative content analysis. Qualitative Health Research, 15(9), 1277–1288. https://doi.org/10.1177/1049732305276687 DOI: https://doi.org/10.1177/1049732305276687

Irawan, E., Rosjanuardi, R., & Prabawanto, S. (2024). Research trends of computational thinking in mathematics learning: A bibliometric analysis from 2009 to 2023. Eurasia Journal of Mathematics, Science and Technology Education, 20(3), 1–16. https://doi.org/10.29333/ejmste/14343 DOI: https://doi.org/10.29333/ejmste/14343

Jonassen, D. H. (1997). Instructional design models for well-structured and ill-structured problem-solving learning outcomes. Educational Technology Research and Development, 45(1), 65–94. https://doi.org/10.1007/bf02299613 DOI: https://doi.org/10.1007/BF02299613

Krippendorff, K. (2004). Content analysis: An introduction to its methodology. In Sage Publications (2nd ed.). Sage Publishers Ltd.

Kynigos, C. (2007). Using half-baked microworlds to challenge teacher educators’ knowing. International Journal of Computers for Mathematical Learning, 12, 87–111. https://doi.org/10.1007/s10758-007-9114-2 DOI: https://doi.org/10.1007/s10758-007-9114-2

Kynigos, C. (2015). Constructionism: Theory of learning or theory of design? In S. J. Cho (Ed.), Selected Regular Lectures from the 12th International Congress on Mathematical Education (pp. 417–438). Springer Cham. https://doi.org/10.1007/978-3-319-17187-6_24 DOI: https://doi.org/10.1007/978-3-319-17187-6_24

Lodi, M., & Martini, S. (2021). Computational thinking, between Papert and Wing. Science & Education, 30(4), 883–908. https://doi.org/10.1007/s11191-021-00202-5 DOI: https://doi.org/10.1007/s11191-021-00202-5

MacPherson, R. T. (1998). Factors affecting technological trouble shooting skills. Journal of Industrial Teacher Education, 35(4), 1–29.

Maharani, S., Kholid, M. N., Pradana, L. N., & Nusantara, T. (2019). Problem solving in the context of computational thinking. Infinity Journal, 8(2), 109–116. https://doi.org/10.22460/infinity.v8i2.p109-116 DOI: https://doi.org/10.22460/infinity.v8i2.p109-116

McCade, J. (1990). Problem Solving: Much More Than Just Design. Journal of Technology Education, 2(1), 1–13. https://doi.org/10.21061/jte.v2i1.a.5 DOI: https://doi.org/10.21061/jte.v2i1.a.5

McCormick, R. (2004). Issues of learning and knowledge in technology education. International Journal of Technology and Design Education, 14(1), 21–44. https://doi.org/10.1023/B:ITDE.0000007359.81781.7c DOI: https://doi.org/10.1023/B:ITDE.0000007359.81781.7c

McKenney, S., & Reeves, T. C. (2018). Conducting educational design research (2nd ed.). Routledge. https://doi.org/10.4324/9781315105642 DOI: https://doi.org/10.4324/9781315105642

McKenney, S., & Reeves, T. C. (2021). Educational design research: Portraying, conducting, and enhancing productive scholarship. Medical Education, 55(1), 82–92. https://doi.org/10.1111/medu.14280 DOI: https://doi.org/10.1111/medu.14280

Mifetu, R. K. (2023). Using activity method to address students’ problem-solving difficulties in circle geometry. Contemporary Mathematics and Science Education, 4(1), 1–8. https://doi.org/10.30935/conmaths/13079 DOI: https://doi.org/10.30935/conmaths/13079

Mohaghegh, M., & Mccauley, M. (2016). Computational Thinking: The skill set of the 21st century. (IJCSIT) International Journal of Computer Science and Information Technologies, 7(3).

Morrison-Love, D. (2022). Technological problem solving: an investigation of differences associated with levels of task success. International Journal of Technology and Design Education, 32(3), 1725–1753. https://doi.org/10.1007/s10798-021-09675-5 DOI: https://doi.org/10.1007/s10798-021-09675-5

Muhammad, R. R., Lawson, D., Aslam, F., & Crawford, M. (2023). Indonesian curriculum 2013 ten years on: Impact on mathematics teaching. Journal of Research in Science, Mathematics and Technology Education, 6(SI), 109–136. https://doi.org/10.31756/jrsmte.616si DOI: https://doi.org/10.31756/jrsmte.616SI

Nordby, S. K., Bjerke, A. H., & Mifsud, L. (2022). Computational thinking in the primary mathematics classroom: A systematic review. Digital Experiences in Mathematics Education, 8(1), 27–49. https://doi.org/10.1007/s40751-022-00102-5 DOI: https://doi.org/10.1007/s40751-022-00102-5

Olsher, S., Abrahamson, D., Arcavi, A., Arzarello, F., Chazan, D., Clark-Wilson, A., Leikin, R., Sinclair, N., & Yerushalmy, M. (2023). Problem solving with technology: Multiple perspectives on mathematical conjecturing. In M. Ayalon, B. Koichu, R. Leikin, L. Rubel, & M. Tabach (Eds.), Proceedings of the 46th Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 134–138). PME.

Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas (1st ed.). Basic Books.

Polat, E., & Yilmaz, R. M. (2022). Unplugged versus plugged-in: Examining basic programming achievement and computational thinking of 6th-grade students. Education and Information Technologies, 27(7), 9145–9179. https://doi.org/10.1007/s10639-022-10992-y DOI: https://doi.org/10.1007/s10639-022-10992-y

Polya, G. (1945). How to solve it. Princeton University Press. DOI: https://doi.org/10.1515/9781400828678

Putra, Z. H., Ramiati, Zufriady, Hidayat, R., Jismulatif, Hermita, N., & Sulistiyo, U. (2022). Development of computational thinking tasks based on Riau Malay culture: A study of fifth-grade public school students in Pekanbaru, Indonesia. Education 3-13, 1–11. https://doi.org/10.1080/03004279.2022.2150063 DOI: https://doi.org/10.1080/03004279.2022.2150063

Resnick, M. (2012). Reviving Papert’s Dream. Educational Technology, 52(4), 42–46.

Resnick, M., Maloney, J., Monroy-Hernández, A., Rusk, N., Eastmond, E., Brennan, K., Millner, A., Rosenbaum, E., Silver, J., Silverman, B., & Kafai, Y. (2009). Scratch: Programming for all. Communications of the ACM, 52(11), 60–67. https://doi.org/10.1145/1592761.1592779 DOI: https://doi.org/10.1145/1592761.1592779

Rijke, W. J., Bollen, L., Eysink, T. H. S., & Tolboom, J. L. J. (2018). Computational thinking in primary school: An examination of abstraction and decomposition in different age groups. Informatics in Education, 17(1), 77–92. https://doi.org/10.15388/infedu.2018.05 DOI: https://doi.org/10.15388/infedu.2018.05

Schaafstal, A., Schraagen, J. M., & van Berl, M. (2000). Cognitive task analysis and innovation of training: The case of structured troubleshooting. Human Factors: The Journal of the Human Factors and Ergonomics Society, 42(1), 75–86. https://doi.org/10.1518/001872000779656570 DOI: https://doi.org/10.1518/001872000779656570

Schoenfeld, A. H. (1985). Mathematical problem solving. Academic Press.

Shute, V. J., Sun, C., & Asbell-Clarke, J. (2017). Demystifying computational thinking. Educational Research Review, 22, 142–158. https://doi.org/10.1016/j.edurev.2017.09.003 DOI: https://doi.org/10.1016/j.edurev.2017.09.003

Sinclair, N. (2001). The Aesthetic Is Relevant. For the Learning of Mathematics, 21(1), 25–32.

Skordialos, E., & Baralis, G. (2017). A teaching approach of geometric shapes’ properties with the use of online educational tools in Greek primary school. New Trends and Issues Proceedings on Humanities and Social Sciences, 4(9), 101–109. https://doi.org/10.18844/prosoc.v4i9.3044 DOI: https://doi.org/10.18844/prosoc.v4i9.3044

Sneider, C., Stephenson, C., Schafer, B., & Flick, L. (2014). Computational thinking in high school science classrooms. The Science Teacher, 81(05), 53–59. https://doi.org/10.2505/4/tst14_081_05_53 DOI: https://doi.org/10.2505/4/tst14_081_05_53

Tokuihsa, S., & Kamiyama, Y. (2010). The World is Canvas: A coloring application for children based on physical interaction. The 9th International Conference on Interaction Design and Children, 315–318. https://doi.org/10.1145/1810543.1810601 DOI: https://doi.org/10.1145/1810543.1810601

Tsukamoto, H., Takemura, Y., Nagumo, H., Ikeda, I., Monden, A., & Matsumoto, K. I. (2015). Programming education for primary school children using a textual programming language. Proceedings - Frontiers in Education Conference, FIE, 1–7. https://doi.org/10.1109/FIE.2015.7344187

Tsukamoto, H., Takemura, Y., Oomori, Y., Ikeda, I., Nagumo, H., Monden, A., & Matsumoto, K. I. (2016). Textual vs. visual programming languages in programming education for primary schoolchildren. Proceedings - Frontiers in Education Conference, FIE, 1–7. https://doi.org/10.1109/FIE.2016.7757571 DOI: https://doi.org/10.1109/FIE.2015.7344187

van Borkulo, S. P., Chytas, C., Drijvers, P., Barendsen, E., & Tolboom, J. (2021). Computational thinking in the mathematics classroom: Fostering algorithmic thinking and generalization skills using dynamic mathematics software. ACM International Conference Proceeding Series, 1–9. https://doi.org/10.1145/3481312.3481319 DOI: https://doi.org/10.1145/3481312.3481319

van den Akker, J., Gravemeijer, K., McKenney, S., & Nieveen, N. (2006). Introducing educational design research. In J. van den Akker, K. Gravemeijer, S. McKenney, & N. Nieveen (Eds.), Educational design research. Routledge. DOI: https://doi.org/10.4324/9780203088364

van Hiele, P. M. (1984). The child’s thought and geometry. In D. Fuys, D. Geddes, & R. Tischler (Eds.), English Translation of Selected Writings of Diana van Hiele-Geldof and Pierre M. van Hiele (pp. 243–252). City University of New York.

Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127–147. https://doi.org/10.1007/s10956-015-9581-5 DOI: https://doi.org/10.1007/s10956-015-9581-5

Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33–35. https://doi.org/10.1145/1118178.1118215 DOI: https://doi.org/10.1145/1118178.1118215

Wu, T.-T., Asmara, A., Huang, Y.-M., & Permata Hapsari, I. (2024). Identification of problem-solving techniques in computational thinking studies: Systematic literature review. Sage Open, 14(2), 1–20. https://doi.org/10.1177/21582440241249897 DOI: https://doi.org/10.1177/21582440241249897

Ye, H., Liang, B., Ng, O.-L., & Chai, C. S. (2023). Integration of computational thinking in K-12 mathematics education: A systematic review on CT-based mathematics instruction and student learning. International Journal of STEM Education, 10(3), 1–26. https://doi.org/10.1186/s40594-023-00396-w DOI: https://doi.org/10.1186/s40594-023-00396-w

Yunianto, W., Cahyono, A. N., Prodromou, T., El-Bedewy, S., & Lavicza, Z. (2024). CT integration in STEAM learning: Fostering students’ creativity by making Batik stamp pattern. Science Activities, 62(1), 26–52. https://doi.org/10.1080/00368121.2024.2378860 DOI: https://doi.org/10.1080/00368121.2024.2378860

Yunianto, W., Sami El-Kasti, H., Charitas Indra Prahmana, R., & Lavicza, Z. (2024). A constructionist approach to learning computational thinking in mathematics lessons. Journal of Information Technology Education: Innovations in Practice, 23, 1–33. https://doi.org/10.28945/5365 DOI: https://doi.org/10.28945/5365

Zhong, B., Wang, Q., Chen, J., & Li, Y. (2016). An exploration of three-dimensional integrated assessment for computational thinking. Journal of Educational Computing Research, 53(4), 562–590. https://doi.org/10.1177/0735633115608444 DOI: https://doi.org/10.1177/0735633115608444

Ziatdinov, R., & Valles, J. R. (2022). Synthesis of modeling, visualization, and programming in GeoGebra as an effective approach for teaching and learning STEM topics. Mathematics, 10(3), 1–16. https://doi.org/10.3390/math10030398 DOI: https://doi.org/10.3390/math10030398