Second graders’ multimodal reasoning in playful inquiry-based mathematics activities

Linn Flaten

doi:10.31129/LUMAT.14.2.2751

Authors

Linn Flaten University of Agder, Norway https://orcid.org/0009-0005-6874-4027

DOI:

https://doi.org/10.31129/LUMAT.14.2.2751

Keywords:

Elementary mathematics, Inquiry, multimodal reasoning, playful learning, semiotic means

Abstract

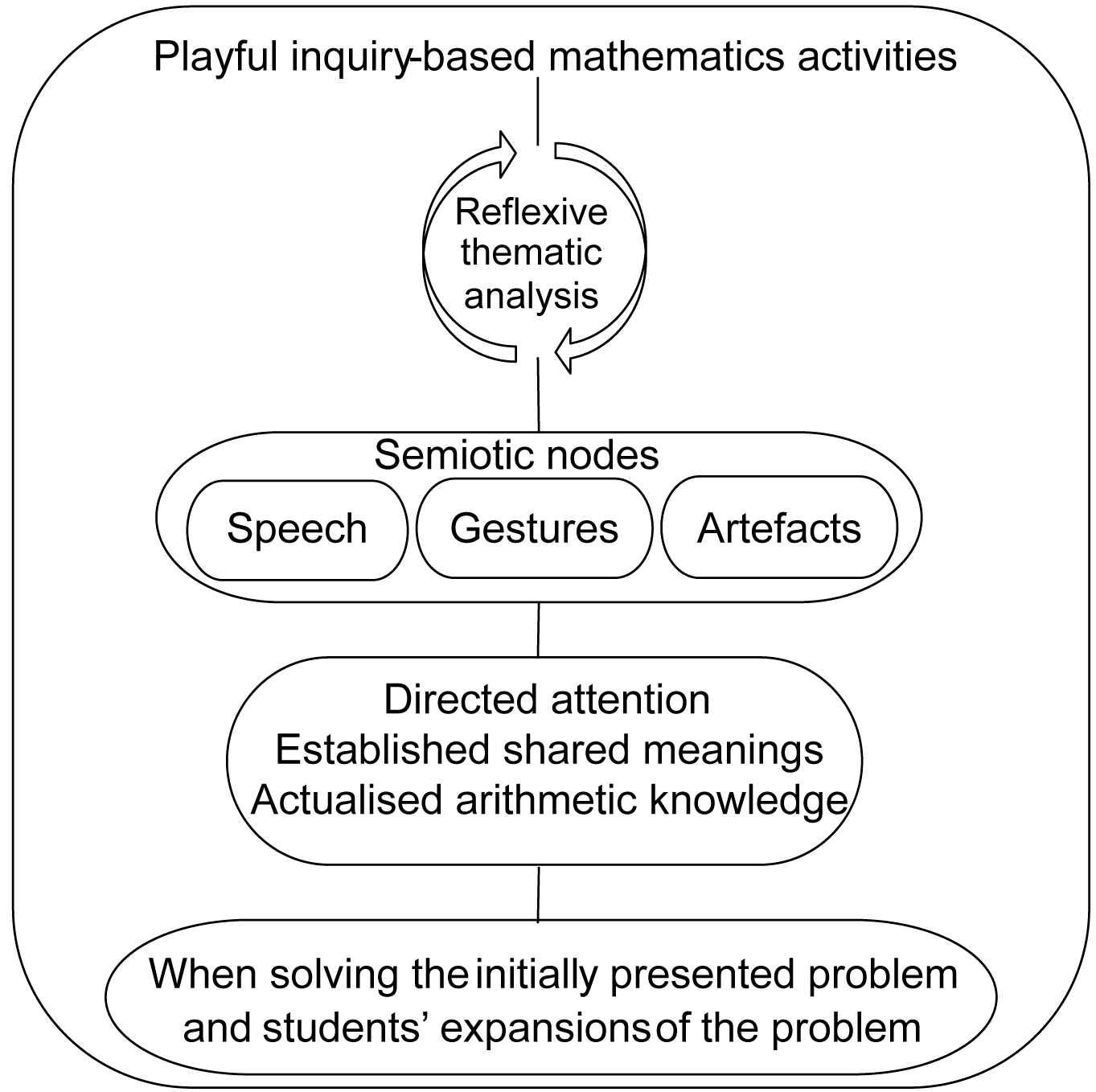
This qualitative study aims to provide insights into lower primary students’ multimodal reasoning from a sociocultural perspective, examining their use of diverse semiotic means of objectification. The pedagogical approach of playful learning was combined with an inquiry approach to engage groups of seven-year-olds in mathematical activities designed collaboratively with participating teachers. Video recordings were generated and transcribed, focusing on participants’ dialogue and actions, and analysed using a reflexive thematic approach. The study shows that the second graders’ multimodal reasoning was characterised by the integration of reasoning words and deixis in speech, synchronised with gestures and the use of artefacts during interactions with peers and the teacher. These three semiotic means emerged as the most prominent cultural tools employed by the students to direct attention, establish shared meanings, and actualise arithmetic knowledge when solving the initial problem and extending it through their own elaborations. The teacher’s balanced involvement supported the reasoning process by responding to the students’ problem expansions and fostering a sense of autonomy in decision-making. Implications are drawn regarding the teacher’s role in guided play.

References

Abdu, R., van Helden, G., Alberto, R., & Bakker, A. (2021). Multimodal dialogue in small-group mathematics learning. Learning, Culture and Social Interaction, 29, 100491. https://doi.org/10.1016/j.lcsi.2021.100491 DOI: https://doi.org/10.1016/j.lcsi.2021.100491

Alibali, M. W., & DiRusso, A. A. (1999). The function of gesture in learning to count: More than keeping track. Cognitive Development, 14(1), 37–56. https://doi.org/https://doi.org/10.1016/S0885-2014(99)80017-3 DOI: https://doi.org/10.1016/S0885-2014(99)80017-3

Bjuland, R., Luiza Cestari, M., & Borgersen, H. E. (2008). The interplay between gesture and discourse as mediating devices in collaborative mathematical reasoning: A multimodal approach. Mathematical Thinking and Learning, 10(3), 271–292. https://doi.org/10.1080/10986060802216169 DOI: https://doi.org/10.1080/10986060802216169

Björklund, C., Magnusson, M., & Palmér, H. (2018). Teachers’ involvement in children’s mathematizing – beyond dichotomization between play and teaching. European Early Childhood Education Research Journal, 26(4), 469–480. https://doi.org/10.1080/1350293X.2018.1487162 DOI: https://doi.org/10.1080/1350293X.2018.1487162

Björklund, C., van den Heuvel-Panhuizen, M., & Kullberg, A. (2020). Research on early childhood mathematics teaching and learning. ZDM – Mathematics Education, 52(4), 607–619. https://doi.org/10.1007/s11858-020-01177-3 DOI: https://doi.org/10.1007/s11858-020-01177-3

Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3(2), 77–101. https://doi.org/10.1191/1478088706qp063oa DOI: https://doi.org/10.1191/1478088706qp063oa

Braun, V., Clarke, V., Hayfield, N., & Terry, G. (2019). Thematic Analysis. In P. Liamputtong (Ed.), Handbook of Research Methods in Health Social Sciences (pp. 843–860). Springer Singapore. https://doi.org/10.1007/978-981-10-5251-4_103 DOI: https://doi.org/10.1007/978-981-10-5251-4_103

Broaders, S. C., Cook, S. W., Mitchell, Z., & Goldin-Meadow, S. (2007). Making children gesture brings out implicit knowledge and leads to learning. Journal of Experimental Psychology, 136(4), 539–550. https://doi.org/10.1037/0096-3445.136.4.539 DOI: https://doi.org/10.1037/0096-3445.136.4.539

Bubikova-Moan, J., Næss Hjetland, H., & Wollscheid, S. (2019). ECE teachers’ views on play-based learning: A systematic review. European Early Childhood Education Research Journal, 27(6), 776–800. https://doi.org/10.1080/1350293X.2019.1678717 DOI: https://doi.org/10.1080/1350293X.2019.1678717

Cobb, P., Confrey, J., diSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9–13. https://doi.org/10.3102/0013189X032001009 DOI: https://doi.org/10.3102/0013189X032001009

Flaten, L. (2025a). Second graders’ problem solving in a playful inquiry-based mathematics activity. Nordic Studies in Mathematics Education, 30(3). https://doi.org/10.7146/nomad.v30i3.157446 DOI: https://doi.org/10.7146/nomad.v30i3.157446

Flaten, L. (2025b). Seven-year-old children’s learning opportunities when solving problems in a playful inquiry-based mathematics activity. European Early Childhood Education Research Journal, 1–17. https://doi.org/10.1080/1350293X.2025.2484240 DOI: https://doi.org/10.1080/1350293X.2025.2484240

Fry, K., Nakar, S., & Zorn, K. (2025). Professional learning interventions for inquiry-based pedagogies in primary classrooms: A scoping review (2012–2022). Mathematics Education Research Journal. https://doi.org/10.1007/s13394-024-00516-x DOI: https://doi.org/10.1007/s13394-025-00557-w

Hirsh-Pasek, K., Golinkoff, R. M., Berk, L., & Singer, D. (2008). A mandate for playful learning in preschool: Presenting the evidence. Oxford University Press. DOI: https://doi.org/10.1093/acprof:oso/9780195382716.001.0001

Jaworski, B. (2005). Learning communities in mathematics: Creating an inquiry community between teachers and didacticians. Research in Mathematics Education, 7(1), 101–119. https://doi.org/10.1080/14794800008520148 DOI: https://doi.org/10.1080/14794800008520148

Jaworski, B. (2006). Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. Journal of Mathematics Teacher Education, 9(2), 187–211. https://doi.org/10.1007/s10857-005-1223-z DOI: https://doi.org/10.1007/s10857-005-1223-z

Jeannotte, D., & Kieran, C. (2017). A conceptual model of mathematical reasoning for school mathematics. Educational Studies in Mathematics, 96(1), 1–16. https://doi.org/10.1007/s10649-017-9761-8 DOI: https://doi.org/10.1007/s10649-017-9761-8

Johansson, M., Lange, T., Meaney, T., Riesbeck, E., & Wernberg, A. (2014). Young children’s multimodal mathematical explanations. ZDM – Mathematics Education, 46(6), 895–909. https://doi.org/10.1007/s11858-014-0614-y DOI: https://doi.org/10.1007/s11858-014-0614-y

Kazemi, E., & Stipek, D. (2001). Promoting conceptual thinking in four upper-elementary mathematics classrooms. The Elementary School Journal, 102(1), 59–80. https://doi.org/10.1086/499693 DOI: https://doi.org/10.1086/499693

Lester, F. K., & Cai, J. (2016). Can mathematical problem solving be taught? Preliminary answers from 30 years of research. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and solving mathematical problems: Advances and new perspectives (pp. 117–135). Springer, Cham. https://doi.org/10.1007/978-3-319-28023-3_8 DOI: https://doi.org/10.1007/978-3-319-28023-3_8

Liljedahl, P., Santos-Trigo, M., Malaspina, U., & Bruder, R. (2016). Problem solving in mathematics education. In P. Liljedahl, M. Santos-Trigo, U. Malaspina, & R. Bruder (Eds.), Problem Solving in Mathematics Education (pp. 1–39). Springer International Publishing. https://doi.org/10.1007/978-3-319-40730-2_1 DOI: https://doi.org/10.1007/978-3-319-40730-2_1

Linell, P. (1998). Approaching dialogue: Talk, interaction and contexts in dialogical perspectives (Vol. 3). John Benjamins. https://doi.org/10.1075/impact.3 DOI: https://doi.org/10.1075/impact.3

McNeill, D. (1992). Hand and mind: What gestures reveal about thought. University of Chicago Press.

McNeill, D. (2005). Gesture and thought (1 ed.). University of Chicago Press. DOI: https://doi.org/10.7208/chicago/9780226514642.001.0001

Mercer, N., & Littleton, K. (2007). Dialogue and the development of children's thinking: A sociocultural approach. Routledge. DOI: https://doi.org/10.4324/9780203946657

Nergård, B. (2023). Preschool children’s mathematical arguments in play-based activities. Mathematics Education Research Journal, 35(1), 193–216. https://doi.org/10.1007/s13394-021-00395-6 DOI: https://doi.org/10.1007/s13394-021-00395-6

Nordin, A.-K., & Boistrup, L. B. (2015, 2015-02-04). Mathematical reasoning through a broad range of communicational resources Ninth Congress of the European Society for Research in Mathematics Education (CERME9), Prague, Czech Republic. https://hal.science/hal-01287696

Nordin, A.-K., & Boistrup, L. B. (2018). A framework for identifying mathematical arguments as supported claims created in day-to-day classroom interactions. The Journal of Mathematical Behavior, 51, 15–27. https://doi.org/10.1016/j.jmathb.2018.06.005 DOI: https://doi.org/10.1016/j.jmathb.2018.06.005

Planas, N., & Pimm, D. (2024). Mathematics education research on language and on communication including some distinctions: Where are we now? ZDM – Mathematics Education, 56(1), 127–139. https://doi.org/10.1007/s11858-023-01497-0 DOI: https://doi.org/10.1007/s11858-023-01497-0

Pyle, A., & Danniels, E. (2017). A continuum of play-based learning: The role of the teacher in play-based pedagogy and the fear of hijacking play. Early Education and Development, 28(3), 274–289. https://doi.org/10.1080/10409289.2016.1220771 DOI: https://doi.org/10.1080/10409289.2016.1220771

Radford, L. (2002). The seen, the spoken and the written: A semiotic approach to the problem of objectification of mathematical knowledge. For the Learning of Mathematics, 22(2), 14–23.

Radford, L. (2003). Gestures, speech, and the sprouting of signs: A semiotic-cultural approach to students' types of generalization. Mathematical Thinking and Learning, 5(1), 37–70. https://doi.org/10.1207/S15327833MTL0501_02 DOI: https://doi.org/10.1207/S15327833MTL0501_02

Radford, L. (2009). Why do gestures matter? Sensuous cognition and the palpability of mathematical meanings. Educational Studies in Mathematics, 70(2), 111–126. https://doi.org/10.1007/s10649-008-9127-3 DOI: https://doi.org/10.1007/s10649-008-9127-3

Radford, L. (2013). Three key concepts of the theory of objectification: Knowledge, knowing, and learning. Journal of Research in Mathematics Education, 2(1), 7–44. https://doi.org/10.4471/redimat.2013.19 DOI: https://doi.org/10.4471/redimat.2013.19

Radford, L. (2014). Towards an embodied, cultural, and material conception of mathematics cognition. ZDM – Mathematics Education, 46(3), 349–361. https://doi.org/10.1007/s11858-014-0591-1 DOI: https://doi.org/10.1007/s11858-014-0591-1

Radford, L. (2021). The theory of objectification: A Vygotskian perspective on knowing and becoming in mathematics teaching and learning (Vol. 4). Brill. https://doi.org/10.1163/9789004459663 DOI: https://doi.org/10.1163/9789004459663

Reynolds, F. J., & Reeve, R. A. (2001). Gesture in collaborative mathematics problem-solving. The Journal of Mathematical Behavior, 20(4), 447–460. https://doi.org/https://doi.org/10.1016/S0732-3123(02)00091-3 DOI: https://doi.org/10.1016/S0732-3123(02)00091-3

Schoenfeld, A. H. (1985). Mathematical problem solving. Academic Press.

Sfard, A., & Kieran, C. (2001). Cognition as communication: Rethinking learning-by-talking through multi-faceted analysis of students' mathematical interactions. Mind, Culture, and Activity, 8(1), 42–76. https://doi.org/10.1207/S15327884MCA0801_04 DOI: https://doi.org/10.1207/S15327884MCA0801_04

Skene, K., O’Farrelly, C. M., Byrne, E. M., Kirby, N., Stevens, E. C., & Ramchandani, P. G. (2022). Can guidance during play enhance children’s learning and development in educational contexts? A systematic review and meta‐analysis. Child Development, 93(4), 1162–1180. https://doi.org/10.1111/cdev.13730 DOI: https://doi.org/10.1111/cdev.13730

Sumpter, L., & Hedefalk, M. (2015). Preschool children's collective mathematical reasoning during free outdoor play. The Journal of Mathematical Behavior, 39, 1–10. https://doi.org/10.1016/j.jmathb.2015.03.006 DOI: https://doi.org/10.1016/j.jmathb.2015.03.006

Säljö, R. (2001). Læring i praksis: Et sosiokulturelt perspektiv [Learning in practice: A sociocultural perspective]. Cappelen Akademisk.

Tabach, M., Hershkowitz, R., Azmon, S., & Dreyfus, T. (2020). Following the traces of teachers’ talk-moves in their students’ verbal and written responses. International Journal of Science and Mathematics Education, 18(3), 509–528. https://doi.org/10.1007/s10763-019-09969-0 DOI: https://doi.org/10.1007/s10763-019-09969-0

van Oers, B. (1996). Are you sure? Stimulating mathematical thinking during young children's play. European Early Childhood Education Research Journal, 4(1), 71–87. https://doi.org/10.1080/13502939685207851 DOI: https://doi.org/10.1080/13502939685207851

van Oers, B. (2010). Emergent mathematical thinking in the context of play. Educational Studies in Mathematics, 74(1), 23–37. https://doi.org/10.1007/s10649-009-9225-x DOI: https://doi.org/10.1007/s10649-009-9225-x

Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Harvard University Press.

Vygotsky, L. S. (1986). Thought and language. MIT Press.

Wathne, U., & Carlsen, M. (2022). Third grade students’ multimodal mathematical reasoning when collaboratively solving combinatorial problems in small groups. Mathematical Thinking and Learning, 26(3), 258–277. https://doi.org/10.1080/10986065.2022.2099611 DOI: https://doi.org/10.1080/10986065.2022.2099611

Webb, N. M., Franke, M. L., Ing, M., Turrou, A. C., Johnson, N. C., & Zimmerman, J. (2019). Teacher practices that promote productive dialogue and learning in mathematics classrooms. International Journal of Educational Research, 97, 176–186. https://doi.org/https://doi.org/10.1016/j.ijer.2017.07.009 DOI: https://doi.org/10.1016/j.ijer.2017.07.009

Weber, K., Maher, C., Powell, A., & Lee, H. S. (2008). Learning opportunities from group discussions: Warrants become the objects of debate. Educational Studies in Mathematics, 68(3), 247–261. https://doi.org/10.1007/s10649-008-9114-8 DOI: https://doi.org/10.1007/s10649-008-9114-8

Weisberg, D. S., Hirsh-Pasek, K., & Golinkoff, R. M. (2013). Guided play: Where curricular goals meet a playful pedagogy. Mind, Brain, and Education, 7(2), 104–112. https://doi.org/10.1111/mbe.12015 DOI: https://doi.org/10.1111/mbe.12015

Weisberg, D. S., Hirsh-Pasek, K., Golinkoff, R. M., Kittredge, A. K., & Klahr, D. (2016). Guided play: Principles and practices. Current Directions in Psychological Science, 25(3), 177–182. https://doi.org/10.1177/0963721416645512 DOI: https://doi.org/10.1177/0963721416645512

Wells, G. (1999). Dialogic inquiry: Towards a sociocultural practice and theory of education. Cambridge University Press. https://doi.org/10.1017/CBO9780511605895 DOI: https://doi.org/10.1017/CBO9780511605895

Wells, G. (2002). The role of dialogue in activity theory. Mind, Culture, and Activity, 9(1), 43–66. https://doi.org/10.1207/S15327884MCA0901_04 DOI: https://doi.org/10.1207/S15327884MCA0901_04

Wells, G. (2007). Semiotic mediation, dialogue and the construction of knowledge. Human Development, 50(5), 244–274. https://doi.org/10.1159/000106414 DOI: https://doi.org/10.1159/000106414

Wester, J. S. (2021). Students’ possibilities to learn from group discussions integrated in whole-class teaching in mathematics. Scandinavian Journal of Educational Research, 65(6), 1020–1036. https://doi.org/10.1080/00313831.2020.1788148 DOI: https://doi.org/10.1080/00313831.2020.1788148

Zosh, J. M., Hirsh-Pasek, K., Hopkins, E. J., Jensen, H., Liu, C., Neale, D., Solis, S. L., & Whitebread, D. (2018). Accessing the inaccessible: Redefining play as a spectrum. Frontiers in Psychology, 9, Article 1124. https://doi.org/10.3389/fpsyg.2018.01124 DOI: https://doi.org/10.3389/fpsyg.2018.01124

Zosh, J. M., Hopkins, E. J., Jensen, H., Liu, C., Neale, D., Hirsh-Pasek, K., Solis, S. L., & Whitebread, D. (2017). Learning through play: A review of the evidence (white paper). https://cms.learningthroughplay.com/media/wmtlmbe0/learning-through-play_web.pdf