Computer-based assessment in mathematics
Issues about validity
DOI:
https://doi.org/10.31129/LUMAT.11.3.1877Keywords:
computer-based assessment, dynamic, interactive, validity, transferAbstract
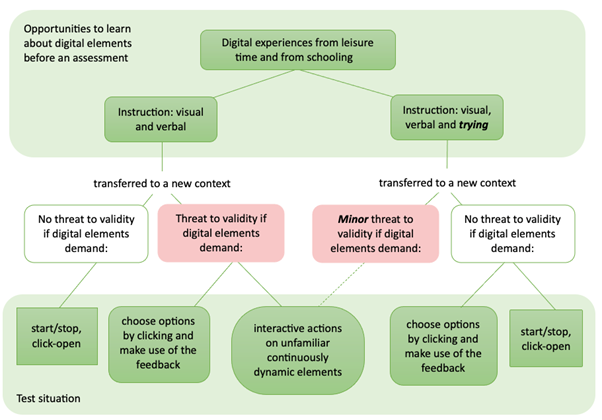
Computer-based assessments is becoming more and more common in mathematics education, and because the digital media entails other demands than paper-based tests, potential threats against validity must be considered. In this study we investigate how preparatory instructions and digital familiarity, may be of importance for test validity. 77 lower secondary students participated in the study and were divided into two groups that received different instructions about five different types of dynamic and/or interactive functions in digital mathematics items. One group received a verbal and visual instruction, whereas the other group also got the opportunity to try using the functions themselves. The students were monitored using eye-tracking equipment during their work with mathematics items with the five types of functions. The result revealed differences in how the students undertook the dynamic functions due to the students’ preparatory instructions. One conclusion is that students need to be very familiar with dynamic and interactive functions in tests, if validity is to be ensured. The validity also depends on the type of dynamic function used.
References
Aldon, G. & Panero, M. (2020). Can digital technology change the way mathematics skills are assessed? ZDM, 52(7), 1333–1348. https://doi.org/10.1007/s11858-020-01172-8 DOI: https://doi.org/10.1007/s11858-020-01172-8
Baccaglini-Frank, A. (2021). To tell a story, you need a protagonist: How dynamic interactive mediators can fulfil this role and foster explorative participation to mathematical discourse. Educational Studies in Mathematics, 106(2), 291–312. https://doi.org/10.1007/s10649-020-10009-w DOI: https://doi.org/10.1007/s10649-020-10009-w
Barana, A., Marchisio, M., & Sacchet, M. (2021). Interactive feedback for learning mathematics in a digital learning environment. Education Sciences, 11(6), 279–290. https://doi.org/10.3390/educsci11060279 DOI: https://doi.org/10.3390/educsci11060279
Bennett, R. E. (2015). The changing nature of educational assessment. Review of Research in Education, 39(1), 370–407. https://doi.org/10.3102/0091732X14554179 DOI: https://doi.org/10.3102/0091732X14554179
Bennett, R. E., Braswell, J., Oranje, A., Sandene, B., Kaplan, B., Yan, F. (2008b). Does it matter if I take my mathematics test on computer? A second empirical study of mode effects in NAEP. Journal of Technology, Learning, and Assessment, 6(9), 1–38.
Bennett, S., Maton, K., & Kervin, L. (2008a). The “digital natives” debate: A critical review of the evidence. British Journal of Educational Technology, 39(5), 775–786. https://doi.org/10.1111/j.1467-8535.2007.00793.x DOI: https://doi.org/10.1111/j.1467-8535.2007.00793.x
Cohen, J. W. (1983). Statistical power analysis for the behavioral sciences (2nd ed.) Lawrence Erlbaum Associates.
College Board. (2022). Assessment framework for the digital SAT suite, version 1.0 (June 2022). College Board.
Dadey, N., Lyons, S., & DePascale, C. (2018). The comparability of scores from different digital devices: A literature review and synthesis with recommendations for practice. Applied Measurement in Education, 31(1), 30–50. https://doi.org/10.1080/08957 347.2017.1391262 DOI: https://doi.org/10.1080/08957347.2017.1391262
Davis, L. L., Morrison, K., Zhou-Yile Schnieders, J., & Marsh, B. (2021). Developing Authentic Digital Math Assessments. Journal of Applied Testing Technology, 22(1), 1–11. Retrieved from http://jattjournal.net/index.php/atp/article/view/155879
Dyrvold, A. (2022). Missed opportunities in digital teaching platforms: Under-use of interactive and dynamic elements. Journal of Computers in Mathematics and Science Teaching, 41(2), 135–161.
Gass, S. M., & Selinker, L. (1983). Language transfer in language learning. Issues in second language research. Newbury House Publishers, Inc.
Geraniou, E., & Jankvist, U.T. (2019). Towards a definition of “mathematical digital competency”. Educ Stud Math 102, 29–45. https://doi.org/10.1007/s10649-019-09893-8 DOI: https://doi.org/10.1007/s10649-019-09893-8
Goldstone, R., Son, J. Y., & Landy, D. (2008). A well grounded education: The role of perception in science and mathematics. Symbols and embodiment (pp. 327–356). Oxford University Press. http://jattjournal.net/index.php/atp/article/view/155879 DOI: https://doi.org/10.1093/acprof:oso/9780199217274.003.0016
Hamhuis, E., Glas, C., & Meelissen, M. (2020). Tablet assessment in primary education: are there performance differences between timss’ paper-and-pencil test and tablet test among dutch grade-four students? British Journal of Educational Technology, 51(6), 2340–2358. https://doi.org/10.1111/bjet.12914 DOI: https://doi.org/10.1111/bjet.12914
Hanho, J. (2014) A comparative study of scores on computer-based tests and paper-based tests. Behaviour & Information Technology, (33)4, 410–422. https://doi.org/10.1080/0144929X.2012.710647 DOI: https://doi.org/10.1080/0144929X.2012.710647
Harris, D., Logan, T., & Lowrie, T. (2021). Unpacking mathematical-spatial relations: Problem-solving in static and interactive tasks. Mathematics Education Research Journal, 33(3), 495–511. https://doi.org/10.1007/s13394-020-00316-z DOI: https://doi.org/10.1007/s13394-020-00316-z
Helsper, E. J., & Eynon, R. (2010). Digital natives: where is the evidence? British Educational Research Journal, 36(3), 503–520. https://doi.org/10.1080/01411920902989227 DOI: https://doi.org/10.1080/01411920902989227
Hoch, S., Reinhold, F., Werner, B., Richter-Gebert, J., & Reiss, K. (2018). Design and research potential of interactive textbooks: the case of fractions. ZDM Mathematics Education, 50(5), 839–848. https://doi.org/10.1007/s11858-018-0971-z DOI: https://doi.org/10.1007/s11858-018-0971-z
Ilovan, O.-R., Buzila, S.-R., Dulama, M. E., & Buzila, L. (2018). Study on the features of geography/sciences interactive multimedia learning activities (IMLA) in a digital textbook. Romanian Review of Geographical Education, 7(1), 20–30. https://doi.org/10.23741/RRGE120182 DOI: https://doi.org/10.23741/RRGE120182
Junpeng, P., Krotha, J., Chanayota, K., Tang, K., & Wilson, M. (2019). Constructing progress maps of digital technology for diagnosing mathematical proficiency. Journal of Education and Learning, 8(6), 90–102. https://doi.org/10.5539/jel.v8n6p90 DOI: https://doi.org/10.5539/jel.v8n6p90
Kaminski, J. A., Sloutsky, V. M., & Heckler, A. F. (2013). The cost of concreteness: The effect of nonessential information on analogical transfer. Journal of Experimental Psychology. Applied, 19(1), 14–29. https://doi.org/10.1037/a0031931 DOI: https://doi.org/10.1037/a0031931
Lemmo, A. (2021). A tool for comparing mathematics tasks from paper-based and digital environments. International Journal of Science and Mathematics Education, 19(8), 1655–1675. https://doi.org/10.1007/s10763-020-10119-0 DOI: https://doi.org/10.1007/s10763-020-10119-0
Lobato, J. (2012). The actor-oriented transfer perspective and its contributions to educational research and practice. Educational Psychologist, 47(3), 232-247. https://doi.org/10.1080/00461520.2012.693353 DOI: https://doi.org/10.1080/00461520.2012.693353
Lobato, J. & Hohense, (2021). Current conceptualisations of the Transfer of learning and their use in STEM education research. In C. Hohensee & J. Lobato (Eds.), Transfer of learning: Progressive perspectives for mathematics education and related fields (pp. 3–26). Springer. DOI: https://doi.org/10.1007/978-3-030-65632-4_1
Lobato, J., & Siebert, D. (2002). Quantitative reasoning in a reconceived view of transfer. The Journal of Mathematical Behavior, 21(1), 87–116. https://doi.org/10.1016/S0732-3123(02)00105-0 DOI: https://doi.org/10.1016/S0732-3123(02)00105-0
Messick, S. (1995). Validity of psychological assessment: Validation of inferences from persons’ responses and performances as scientific inquiry into score meaning. American psychologist, 50(9), 741–749. DOI: https://doi.org/10.1037/0003-066X.50.9.741
Mullis, I. V. S., & Martin, M. O. (Eds.). (2017). TIMSS 2019 Assessment Frameworks. Retrieved from Boston College, TIMSS & PIRLS International Study Center website: http://timssandpirls.bc.edu/timss2019/frameworks
Nathan, M. J. & Alibali, M. W. (2021). An embodied theory of transfer of mathematical learning. In C. Hohensee & J. Lobato (Eds.), Transfer of learning: Progressive perspectives for mathematics education and related fields (pp. 27–58). Springer. DOI: https://doi.org/10.1007/978-3-030-65632-4_2
OECD (2013), PISA 2012 Assessment and Analytical Framework: Mathematics, Reading, Science, Problem Solving and Financial Literacy, OECD Publishing. http://dx.doi.org/10.1787/9789264190511-en
OECD (2021). 21st-Century Readers: Developing Literacy Skills in a Digital World. PISA, OECD Publishing. http://dx.doi.org/10.1787/9789264190511-en DOI: https://doi.org/10.1787/9789264190511-en
O’Halloran, K. L., Beezer, R. A., & Farmer, D. W. (2018). A new generation of mathematics textbook research and development. ZDM Mathematics Education, 50(5), 863–879. https://doi.org/10.1007/s11858-018-0959-8 DOI: https://doi.org/10.1007/s11858-018-0959-8
Prensky, M. (2001). Digital Natives, Digital Immigrants. On the Horizon, 9(5), 1–6. DOI: https://doi.org/10.1108/10748120110424816
Regeringen (2017). Uppdrag att digitalisera de nationella proven. https://www.regeringen.se/4a80ac/contentassets/03dee5c5cdf244afa053e26cf654a8d8/uppdrag-att-digitalisera-de-nationella-proven-m.m..pdf
Ripley, M. (2009). Transformational computer-based testing. In F. Scheuermann & J. Björnsson (Eds.), The transition to computer-based assessment (pp. 92–98). Office for Official Publications of the European Communities
Smolinsky, L., Marx, B. D., Olafsson, G., & Ma, Y. A. (2020). Computer-based and paper-and-pencil tests: A study in calculus for STEM majors. Journal of Educational Computing Research, 58(7), 1256–1278. https://doi.org/10.1177/0735633120930235 DOI: https://doi.org/10.1177/0735633120930235
Thorndike, E. L., & Woodworth, R. S. (1901). The influence of improvement in one mental function upon the efficiency of other functions. Psychological Review, 8, 247–261. DOI: https://doi.org/10.1037/h0074898
Usiskin, Z. (2018). Electronic vs. paper textbook presentations of the various aspects of mathematics. ZDM Mathematics Education, 50(5), 849–861. https://doi-org.ezproxy.its.uu.se/10.1007/s11858-018-0936-2 DOI: https://doi.org/10.1007/s11858-018-0936-2
Yerushalmy, M., & Olsher, S. (2020). Online assessment of students’ reasoning when solving example-eliciting tasks: Using conjunction and disjunction to increase the power of examples. ZDM Mathematics Education, 52(5), 1033–1049. https://doi.org/10.1007/s11858-020-01134-0 DOI: https://doi.org/10.1007/s11858-020-01134-0
Downloads
Published
How to Cite
Issue
Section
Categories
License
Copyright (c) 2023 Anneli Dyrvold, Ida Bergvall

This work is licensed under a Creative Commons Attribution 4.0 International License.









