Programming as a mediator of mathematical thinking
Examples from upper secondary students exploring the definite integral
DOI:
https://doi.org/10.31129/LUMAT.12.3.2155Keywords:
collaborative learning, definite integral, languaging, programming, sociomathematical normsAbstract
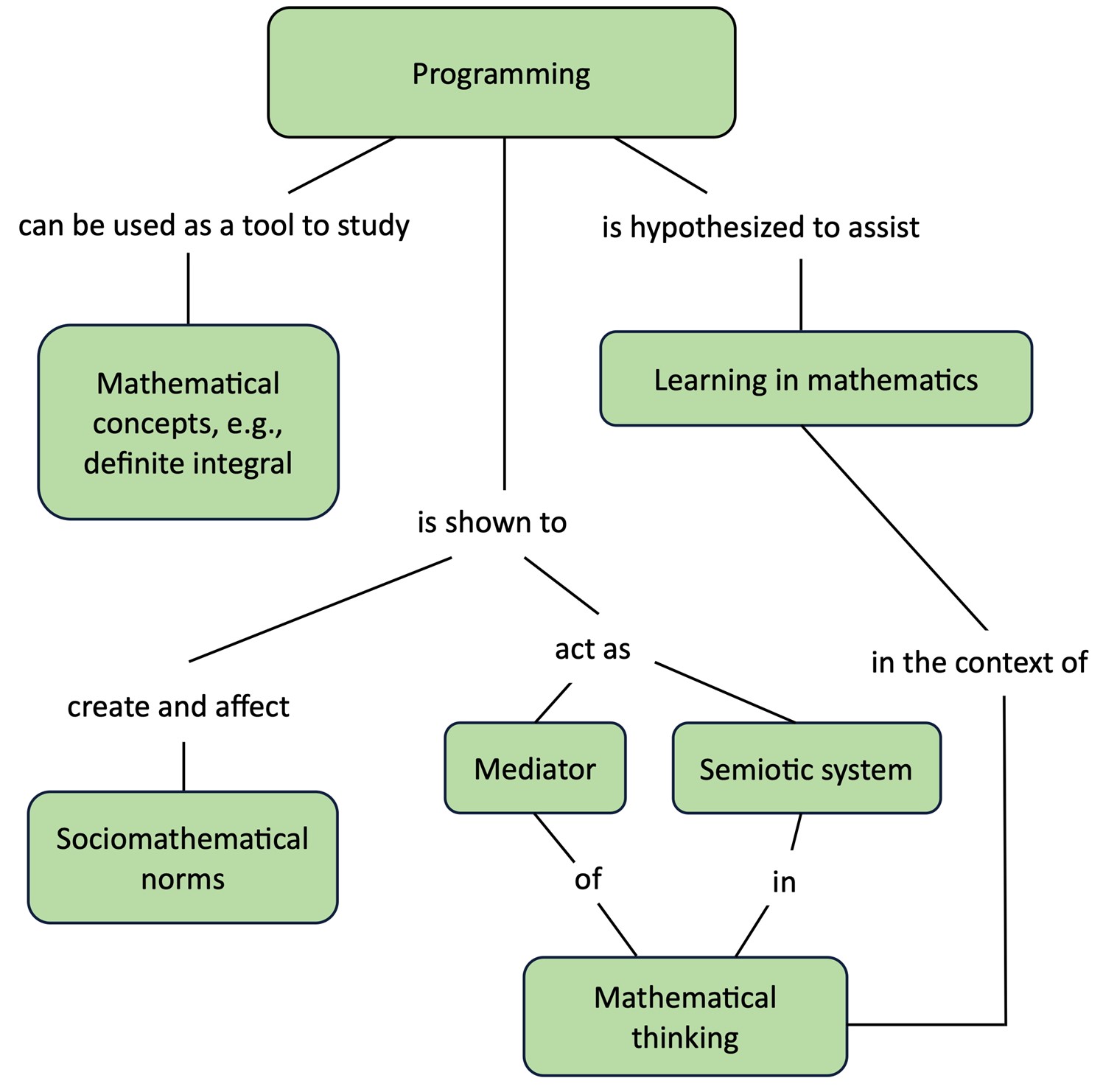
We report on three episodes from a case study where upper secondary students numerically explore the definite integral in a Python environment. Our research questions concern how code can mediate and support students' mathematical thinking and what kind of sociomathematical norms emerge as students work together to reach a mutual understanding of a correct solution. The main findings of our investigation are as follows. 1) Students can actively use code as a mediator of their mathematical thinking, and code can even serve as a bridge that helps students to develop their mathematical thinking collaboratively. Further, code can help students to perceive mathematical notions as objects with various properties and to communicate about these properties, even in other semiotic systems than the mathematical language. 2) For the participating students, a common norm was that an acceptable solution is a sufficient condition for the correctness of the solution method although students were aware of a problem in their code, yet also other norms emerged. This demonstrates that learning mathematics with programming can have an effect on what kind of sociomathematical norms emerge in classroom.
References
Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Roa Fuentes, S., Trigueros, M., & Weller, K. (2014). APOS Theory. A framework for Research and Curriculum Development in Mathematics Education. Springer. https://doi.org/10.1007/978-1-4614-7966-6 DOI: https://doi.org/10.1007/978-1-4614-7966-6
Attorps, I., Björk, K., Radic, M., & Tossavainen, T. (2010). The learning study model and the teaching of the definite integral concept. In M. Asikainen, P. E. Hirvonen, & K. Sormunen (Eds.), Ajankohtaista matemaattisten aineiden opetuksen ja oppimisen tutkimuksessa. Matematiikan ja luonnontieteiden opetuksen tutkimuspäivät Joensuussa 22.-23.10.2009. Reports and Studies in Education, Humanities, and Theology (pp. 77–86). University of Eastern Finland.
Attorps, I., Björk, K., Radic, M., & Tossavainen, T. (2013). Varied ways to teach the definite integral concept. International Electronic Journal of Mathematics Education, 8(2–3), 81–99. DOI: https://doi.org/10.29333/iejme/275
Drijvers, P. (2018). Empirical evidence for benefit? Reviewing quantitative research on the use of digital tools in mathematics education. In L. Ball, P. Drijvers, S. Ladel, H-S. Siller, M. Tabach, & C. Vale (Eds.), Uses of technology in primary and secondary mathematics education (pp. 161–175). Springer. https://doi.org/10.1007/978-3-319-76575-4_9 DOI: https://doi.org/10.1007/978-3-319-76575-4_9
Forsström, S. E., & Kaufmann, O. T. (2018). A literature Review exploring the use of programming in mathematics education. International Journal of Learning, Teaching and Educational Research, 17(12), 18–32. https://doi.org/10.26803/ijlter.17.12.2 DOI: https://doi.org/10.26803/ijlter.17.12.2
Güven, N. D., & Dede, Y. (2017). Examining social and sociomathematical norms in different classroom microcultures: Mathematics teacher education perspective. Educational Sciences: Theory & Practice, 17(1), 265–292. https://doi.org/10.12738/estp.2017.1.0383 DOI: https://doi.org/10.12738/estp.2017.1.0383
Johansson, C., Juhlin, A., Tossavainen, T., & Wedestig, A. (2023). Nyfikenhet och tillräcklighet. Gymnasielärares erfarenheter av att undervisa matematik med programmering. Nämnaren, 49(3), 35–41.
Jones, S. R. (2018). Prototype images in mathematics education: the case of the graphical representation of the definite integral. Educational Studies in Mathematics, 97(3), 215–234. https://doi.org/10.1007/s10649-017-9794-z DOI: https://doi.org/10.1007/s10649-017-9794-z
Joutsenlahti, J., & Kulju, P. (2017). Multimodal languaging as a pedagogical model—A case study of the concept of division in school mathematics. Education Sciences, 7(1), 9. https://doi.org/ 10.3390/educsci7010009 DOI: https://doi.org/10.3390/educsci7010009
Joutsenlahti, J. & Tossavainen, T. (2018). Matemaattisen ajattelun kielentäminen ja siihen ohjaaminen koulussa. In J. Joutsenlahti, H. Silfverberg & P. Räsänen (Eds.), Matematiikan opetus ja oppiminen (pp. 410–430). Niilo Mäki Instituutti.
Kilhamn, C., Rolandsson, L., & Bråting, K. (2021). Programmering i svensk skolmatematiken? LUMAT – International Journal on Math, Science and Technology Education, 9(1), 283–312. https://doi.org/10.31129/LUMAT.9.2.1457 DOI: https://doi.org/10.31129/LUMAT.9.2.1457
Krippendorff, K. (2018). Content analysis: An introduction to its methodology (Fourth edition). Sage. https://doi.org/10.4135/9781071878781 DOI: https://doi.org/10.4135/9781071878781
Misfeldt, M., Jankvist, U.T., Geraniou, E., & Bråting, K. (2020). Relations between mathematics and programming in school: Juxtaposing three different cases. In A. Donevska-Todorova, E. Faggiano, J. Trgalova, Z. Lavicza, R. Weinhandl, A. Clark-Wilson & H-G. Weigand (Eds.), Proceedings of the 10th ERME topic conference on mathematics education in the digital era (MEDA 2020), (s. 255–262). Johannes Kepler University.
Morgan, C., Craig, T., Schuette, M., & Wagner, D. (2014). Language and communication in mathematics education: An overview of research in the field. ZDM, 46(6), 843–853. https://doi.org/10.1007/s11858-014-0624-9 DOI: https://doi.org/10.1007/s11858-014-0624-9
Moschkovich, J. N. (2021). Learners’ language in mathematics classrooms: What we know and what we need to know. In N. Planas, C. Morgan & M. Schütte (Eds.), Classroom research on mathematics and language: Seeing learners and teachers differently; classroom research on mathematics and language: Seeing learners and teachers differently (pp. 60–76). Routledge/Taylor & Francis Group. https://doi.org/10.4324/9780429260889-5 DOI: https://doi.org/10.4324/9780429260889-5
Olsson, J., & Granberg, C. (2022). Teacher-student interaction supporting students’ creative mathematical reasoning during problem solving using Scratch. Mathematical Thinking and Learning, Advance online publication. https://doi.org/10.1080/10986065.2022.2105567 DOI: https://doi.org/10.1080/10986065.2022.2105567
Olteanu, C. (2022). Programming, mathematical reasoning and sense-making. International Journal of Mathematical Education in Science and Technology, 53(8), 2046–2064. https://doi.org/10. 1080/0020739x.2020.1858199 DOI: https://doi.org/10.1080/0020739X.2020.1858199
Ozdemir Baki, G., & Kilicoglu, E. (2023). Social and socio-mathematical norms constructed by teachers in classes through the development of noticing skills. International Electronic Journal of Mathematics Education, 18(1), em0723. https://doi.org/10.29333/iejme/12649 DOI: https://doi.org/10.29333/iejme/12649
Partanen, A. M., & Kaasila, R. (2015). Sociomathematical norms negotiated in the discussions of two small groups investigating calculus. International Journal of Science and Mathematics Education, 13(4), 927–946. https://doi.org/10.1007/s10763-014-9521-5 DOI: https://doi.org/10.1007/s10763-014-9521-5
Planas, N. & Pimm, D. (2024). Mathematics education research on language and on communication including some distinctions: Where are we now? ZDM – Mathematics Education, 56, 127–139. https://doi.org/10.1007/s11858-023-01497-0 DOI: https://doi.org/10.1007/s11858-023-01497-0
Rasslan, S., & Tall, D. (2002). Definitions and images for the definite integral concept. In A. Cockburn & E. Nardi (Eds.), Proceedings of the 26th International Conference for the Psychology of Mathematics Education (Vol. 4, pp. 89–96). Norwich, UK.
Tossavainen, T., & Faarinen, E. C. (2019). Swedish fifth and sixth graders’ motivational values and the use of ICT in mathematics education. Eurasia Journal of Mathematics, Science and Technology Education, 15(12), em1776. https://doi.org/10.29333/ejmeste/108533 DOI: https://doi.org/10.29333/ejmste/108533
Tossavainen, T., Rensaa, R. J., Haukkanen, P., Mattila, M., & Johansson, M. (2020). First-year engineering students’ mathematics task performance and its relation to their motivational values and views about mathematics. European Journal of Engineering Education, 46(4), 604–617. https://doi.org/10.1080/03043797.2020.1849032 DOI: https://doi.org/10.1080/03043797.2020.1849032
Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27, 458–477. https://doi.org/10.2307/749877 DOI: https://doi.org/10.5951/jresematheduc.27.4.0458
Yackel, E., Cobb, P., & Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. Journal for Research in Mathematics Education, 22(5), 390–408. DOI: https://doi.org/10.5951/jresematheduc.22.5.0390
Downloads
Published
How to Cite
License
Copyright (c) 2024 Timo Tossavainen, Claes Johansson, Alf Juhlin, Anna Wedestig

This work is licensed under a Creative Commons Attribution 4.0 International License.









